F# Advent - Functional Motor Control
TL;DR I implemented a proportional-integral feedback controller to control the speed of a DC motor using a gyroscope. I wrote it in F# using a functional programming style. The work was easily ported to run on Wilderness Labs’ Meadow IoT hardware.

In this blog I would like to implement a simple but robust control theory that was taught to me in college. This blog post is one in a series of “F# Advent” posts coordinated by Sergey Tihon so I will be implementing it all using my favorite programming language F#.
Embedded controls such as these are often implemented in imperative languages like C with a lot of variable mutation.
I want to explore implementing a DC motor control algorithm in functional style instead of the imperative style. I also want to do it while embracing F#’s strong type checking and units of measure support.
I will try to spare you the heavy math but this is definitely going to be a nerdy post. Enjoy!
Motor control
Motors are some of the simplest but most entertaining devices out there to play with. You can use them to make cars, clocks, drones, and automatic fidget spinners.
The technique I’m going to describe here is a general one that can be applied to a variety of control tasks, not just motors.
It’s a three step process:
- We look at the inputs and outputs
- We compare the output to what we want
- We modify the input to get us closer to the output
Easy peasy! That’s the general outline. There is of course a million ways to accomplish all of the above. So let’s start with the easy stuff: inputs.
Inputs
I am using a DC motor with two pins. When one pin’s voltage is higher than the other, the motor spins one way. When it’s lower, the motor spins the other way.
But I won’t actually be controlling the motor using voltages, instead I’m going to be using a square wave with a varying duty cycle called a PWM (pulse width modulation) to mimic different voltages.
By changing how often a digital pin is on and off, I can mimic analog voltages. If I have a duty cycle of 100%, then the motor will be given all the voltage my circuit can muster. If I give it a duty cycle of 50%, then it will get half that voltage. A duty cycle of 0% would mean the voltage is 0 V.
Let’s model the motor input. I’m going to take advantage of F#’s unit system to make sure all my math and my functions are physically correct.
[<Measure>]
type percent
type MotorInput =
{
ClockwiseDutyCycle : float<percent>
CounterClockwiseDutyCycle : float<percent>
}
member this.DirectionalDutyCycle =
this.ClockwiseDutyCycle - this.CounterClockwiseDutyCycle
let makeMotorInput (cw : float<percent>) (ccw : float<percent>) =
{
ClockwiseDutyCycle = max (min cw 100.0<percent>) 0.0<percent>
CounterClockwiseDutyCycle = max (min ccw 100.0<percent>) 0.0<percent>
}
I created a helper function makeMotorInput that ensures the duty cycles are in a valid range.
While motors are controlled with two pins, they are usually easier to reason about using positive numbers to go in one direction and negative numbers to go in the other. I’m going to create a function to implement that.
let makeDirectionalMotorInput (directionalDutyCycle : float<percent>) =
if directionalDutyCycle >= 0.0<percent> then
makeMotorInput directionalDutyCycle 0.0<percent>
else
makeMotorInput 0.0<percent> (-directionalDutyCycle)
[makeDirectionalMotorInput (101.0<percent>)
makeDirectionalMotorInput (50.0<percent>)
makeDirectionalMotorInput (0.0<percent>)
makeDirectionalMotorInput (-101.0<percent>)]
| index | ClockwiseDutyCycle | CounterClockwiseDutyCycle | DirectionalDutyCycle |
|---|---|---|---|
| 0 | 100 | 0 | 100 |
| 1 | 50 | 0 | 50 |
| 2 | 0 | 0 | 0 |
| 3 | 0 | 100 | -100 |
We have a lot of good code now to work with inputs, let’s look at the outputs of the motor.
Outputs
When it comes to motors we can control any of these things:
- Its position
- Its speed
- Its acceleration
But we can only control them if we can measure them. If we want to control the position of a motor, to control, say, a door, then we need a way to measure its position. In that case, either its angular position or the position of a part of the door.
You can also control its acceleration or the force it produces against an object. But as my controls professor always said, “don’t try to control forces”. So, I’ll leave that as an exercise for the reader.
Controlling the speed of a motor is probably the most common scenario. There are multiple sensors you can use to measure the speed: you could use the same position sensors and do some math, you can use rotary encoders, you can measure minor fluctuation is voltages produced by the motor, you can use potentiometers, … There are a lot of options.
I’m going to use a less common sensor to measure the rotation of the motor: a gyroscope. Gyroscopes measure angular velocity, just what I want. They’re more complicated to use than the other options, but I think they’re fun so I’m going to use them in this project. I will be using an MPU6050 that is capable of measuring linear accelerations and angular velocities on all three axes. I’ll just be monitoring the one rotational axis.
/// Radians
[<Measure>]
type rpm
type MotorOutput = float<rpm>
Control Algorithm
Now that we have defined our inputs and outputs we can discuss how to control the motor to achieve desired speed.
The standard negative feedback control loop looks like this:
- Read outputs:
let outputs = getOutputs () - Calculate error:
let error = desiredOutputs - realOutputs - Calculate new inputs:
setInputs (lastInput + control error)
This three-part loop is general purpose enough to solve any control problem where you’re trying to achieve a measurable goal.
The real magic happens in the function control. It is responsible for deciding what the inputs should be to the
motor based upon how far off we are from our desired speed. This kind of controller is called a regulating controller because it’s designed to bring whatever error it is given down to 0. It does that by increasing the input when the error gets larger and decreasing it when it’s smaller.
type ControlError = float<rpm>
One simple way to implement the controller is to make the input proportional to the error:
let controlWithProportionalResponse (proportion : float<percent/rpm>) (error : ControlError) =
proportion * error
Proportional control makes a lot of intuitive sense: if we want the motor to go faster then we should give it more voltage. If we want it to go slower, then we should give it less.
This kind of control certainly works, but it has some negative side effects. First, it’s tricky decide what that proportion should be. Trial and error is often used though I will discuss alternatives to trial and error later. But worse than that, it’s jittery! The control will never be happy as it always has some error and will always force the motor to jitter back and forth as it tries to meet the desired output.
What we need is a calming influence. Something called an integral controller.
Integral control doesn’t act unless the error has accumulated for a bit of time. It’s slower acting than the proportional controller, but it is easier to tune and really helps the controller to relax when it’s near the desired output. The formal definition of the controller involves integrating the error. Integrating is just a fancy word for adding a bunch of things up. We’re going to add up the error. But we’re not going to do it forever, just the last few seconds worth of error. To do that, I’m going to create a datatype that can keep track of everything.
type ErrorIntegral =
{
MaxErrors : int
Errors : ControlError list
}
member this.TotalError = List.sum this.Errors
member this.NumErrors = this.Errors.Length
member this.LastError = match this.Errors with x :: _ -> x | _ -> 0.0<rpm>
member this.Add error =
{ this with
Errors =
let n = this.Errors.Length
if n < this.MaxErrors then
error :: this.Errors
else
error :: (this.Errors.[..(n-2)])
}
let makeErrorIntegral (maxErrors : int) =
{
MaxErrors = maxErrors
Errors = []
}
Let’s test it out by creating one that can only hold 2 errors.
let ei = makeErrorIntegral 2
ei
| MaxErrors | Errors | TotalError | NumErrors | LastError |
|---|---|---|---|---|
2 | [ ] | 0 | 0 | 0 |
let ei3 = ei.Add(100.0<rpm>).Add(200.0<rpm>).Add(300.0<rpm>)
ei3
| MaxErrors | Errors | TotalError | NumErrors | LastError |
|---|---|---|---|---|
2 | [ 300, 200 ] | 500 | 2 | 300 |
ei3.LastError
We can see that it discarded the first error when the third error arrived.
Now that we have an integrator, we can write the integral control function:
let controlWithIntegralResponse (proportion : float<percent/rpm>)
(errorIntegral : ErrorIntegral) =
proportion * errorIntegral.TotalError
This integral controller still has a proportion parameter because we still want to be able to tune how aggressive or passive the controller is.
We can combine these two controllers to get the best of both worlds. This proportional-integral controller is called a PI controller in control theory.
let control (kp : float<_>) (ki : float<_>) (errors : ErrorIntegral) =
let p = controlWithProportionalResponse kp errors.LastError
let i = controlWithIntegralResponse ki errors
p + i
Hardware Abstraction
In order to test this controller and implement in hardware, I will define a hardware abstraction layer in the form of an interface.
type IHardware =
abstract GetOutput : unit -> MotorOutput
abstract SetInput : MotorInput -> unit
This is the only mutable object in the code and it’s mutable because real hardware is mutable. Once you have performed an action on it, it’s impossible to undo that action.
Let’s also define some test hardware so we can validate our algorithms.
type TestHardware (initialOutput : MotorOutput) =
let mutable output = initialOutput
let mutable input = 0.0<percent>
interface IHardware with
member this.GetOutput () =
output <- (output + input * 100.0<rpm/percent>) * 0.5
printfn "Test Speed: %.3f RPM" (float output)
output
member this.SetInput newInput =
input <- newInput.DirectionalDutyCycle
With that simple abstraction, we can implement the control loop.
Function Control Loop
I am going to implement the control loop as a classic fold operation over an infinite sequence of time.
This architecture keeps the control loop nice and functional and makes it very easy to test different states.
In order to use fold, you need three things:
- Sequence - I will use time
- State - I will track the last input and the error integral
- Transformer - This is the control algorithm
Let’s start by defining the control loop:
/// Seconds
[<Measure>]
type s
type ControlState = MotorInput * ErrorIntegral
let controlLoop (hardware : IHardware) (kp : float<_>) (ki : float<_>)
(desiredOutput : float<s> -> MotorOutput)
((lastInput, errors) : ControlState)
((t, output) : float<s> * MotorOutput) =
let error = desiredOutput t - output
let newErrors = errors.Add error
let newInputDutyCycle = lastInput.DirectionalDutyCycle + control kp ki newErrors
let newInput = makeDirectionalMotorInput newInputDutyCycle
hardware.SetInput newInput
newInput, newErrors
For the sequence I am going to create a general purpose sampler that calls a function to read some data over fixed time intervals. It even blocks the thread for those intervals to keep things in real time.
let sampler (dt : float<s>) (sample : float<s> -> 'a) =
seq {
let sw = System.Diagnostics.Stopwatch ()
sw.Start ()
while true do
yield sample (sw.Elapsed.TotalSeconds * 1.0<s>)
System.Threading.Thread.Sleep (TimeSpan.FromSeconds (float dt))
}
let time = sampler 0.1<s> (fun t -> t)
time |> Seq.take 3
| index | value |
|---|---|
| 0 | 3E-07 |
| 1 | 0.1036857 |
| 2 | 0.2037907 |
We can use that sampler to sample the outputs of the motor.
type MotorSampler = (float<s> * MotorOutput) seq
let motorSampler dt (hardware : IHardware) : MotorSampler =
sampler dt (fun t -> t, hardware.GetOutput ())
Let’s test it out.
let testOutputs = motorSampler 0.1<s> (new TestHardware (100.0<rpm>))
testOutputs |> Seq.take 3
Test Speed: 50.000 RPM
Test Speed: 25.000 RPM
Test Speed: 12.500 RPM
| index | Item1 | Item2 |
|---|---|---|
| 0 | 3E-07 | 50 |
| 1 | 0.1064288 | 25 |
| 2 | 0.2124844 | 12.5 |
That’s working great! Now let’s put it all together.
let controlMotor (maxIterations : int) (integralIterations : int)
(hardware : IHardware) (kp : float<_>) (ki : float<_>)
(desiredOutput : float<s> -> MotorOutput) =
let loop = controlLoop hardware kp ki desiredOutput
let initialState = makeDirectionalMotorInput 0.0<percent>,
makeErrorIntegral integralIterations
let motorOutputs = motorSampler 0.1<s> hardware
motorOutputs
|> Seq.take maxIterations
|> Seq.fold loop initialState
|> ignore
We can now run a test to see if we can control the test hardware. Let’s try to get it up to 100.0<rpm>.
let testGoals (t : float<s>) = if t < 1.5<s> then 100.0<rpm> else 0.0<rpm>
controlMotor 30 3 (new TestHardware (0.0<rpm>)) 0.002<_> 0.0002<_> testGoals
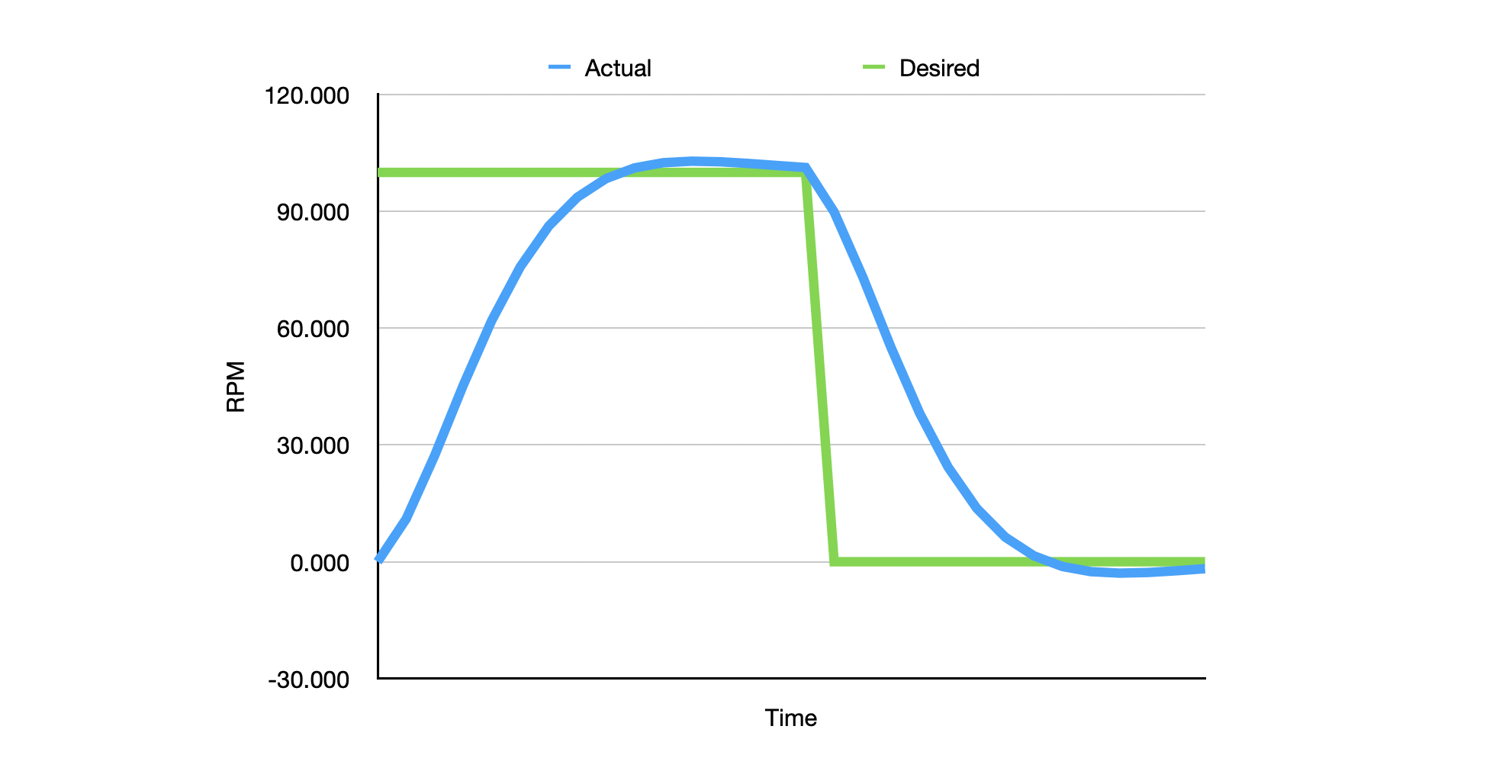
Test Speed: 0.000 RPM
Test Speed: 11.000 RPM
Test Speed: 27.290 RPM
Test Speed: 45.323 RPM
Test Speed: 61.971 RPM
Test Speed: 75.752 RPM
Test Speed: 86.237 RPM
Test Speed: 93.616 RPM
Test Speed: 98.388 RPM
Test Speed: 101.153 RPM
Test Speed: 102.488 RPM
Test Speed: 102.887 RPM
Test Speed: 102.732 RPM
Test Speed: 102.301 RPM
Test Speed: 101.776 RPM
Test Speed: 101.267 RPM
Test Speed: 89.833 RPM
Test Speed: 73.204 RPM
Test Speed: 54.926 RPM
Test Speed: 38.115 RPM
Test Speed: 24.235 RPM
Test Speed: 13.699 RPM
Test Speed: 6.301 RPM
Test Speed: 1.529 RPM
Test Speed: -1.225 RPM
Test Speed: -2.546 RPM
Test Speed: -2.929 RPM
Test Speed: -2.761 RPM
Test Speed: -2.318 RPM
Test Speed: -1.785 RPM
That worked! You can see that the controller even overshot the mark and then had to backtrack.
You can play with the kp and ki values to see how different values affect how quickly the controller speeds up the motor.
Real Hardware
With the abstract interface IHardware, it’s very easy to run this code on real hardware.
To demonstrate this, I’m going to code against the Meadow F7 Board from Wilderness Labs. This board runs .NET code including F# so is a perfect digital controller for this application.
The board uses the Meadow API that has abstractions for all sorts of hardware.
open Meadow
open Meadow.Devices
type MotorMeadowApp() =
inherit App<F7Micro, MotorMeadowApp>()
let device = MotorMeadowApp.Device
let i2c = device.CreateI2cBus()
let mpu = new Meadow.Foundation.Sensors.Motion.Mpu6050(i2c)
do
mpu.Wake()
mpu.StartUpdating (1000 / 50)
let motorCwPwm = device.CreatePwmPort(device.Pins.D09, 200.0f, 1.0f)
let motorCcwPwm = device.CreatePwmPort(device.Pins.D10, 200.0f, 0.0f)
do
motorCwPwm.Start()
motorCcwPwm.Start()
interface IHardware with
member this.GetOutput () =
(float mpu.YGyroscopicAcceleration) / 360.0 * 60.0<rpm>
member this.SetInput newInput =
motorCwPwm.DutyCycle <-
float32 (newInput.ClockwiseDutyCycle / 100.0<percent>)
motorCcwPwm.DutyCycle <-
float32 (newInput.CounterClockwiseDutyCycle / 100.0<percent>)
In just 20 lines of code I was able to implement the IHardware interface. For details, I hope you’ll check out the Meadow Documentation.
Now it’s a matter of executing the control loop:
[<EntryPoint>]
let main argv =
printfn "Motor Control from F#!"
let app = new MotorMeadowApp()
controlMotor int.MaxValue 3 app 0.002<_> 0.0002<_> testGoals
0
For details, I hope you’ll check out the Meadow Documentation.
Conclusion
I hope you enjoyed this functional look into control theory using my favorite language F#.
We were able to build a strongly typed code base to control the speed of a motor with minimal mutation. I hope this code demonstrates some of the benefits functional programming can bring to a space that is generally dominated by procedural programming.
This was my also my first F# Advent post. I hope you enjoyed it and are staying safe and healthy!